Introduction

“How people approach life is a part of culture and culture is strongly affected by climate. Climate doesn’t make a person, but it is one part of what influences each of us. We believe it shapes the culture in important ways.”

Dr. Paul van Lange, a professor of psychology at the Vrije Universiteit Amsterdam (VU)

Github R-Script

Weather has long been rumored to be a significant factor in the prevalence and frequency of crime. Some scientists have started focusing on this as a way gauge and map behavioral changes and find causations in patterns of violent activity.

In one example a team of researchers has developed a new model to better explain why violent crime rates are consistently higher near the equator compared to other parts of the world.

The new model, called CLASH (Climate Aggression, and Self-control in Humans), moves well beyond the simple fact that heat is linked to aggressive behavior. It suggests that a hot climate combined with less variation in seasonal temperatures can lead to a faster life strategy, less focus on the future, and less self-control, all of which contribute to aggression and violence.

The model is built around the Routine Activity Theory which suggests that since people are outdoors and interacting more with others in warm weather, they naturally run into more opportunities for conflict. But this still doesn’t explain why there’s more violence when the temperature is 95 degrees F than when it is 75 degrees F, even though people might be outside under both circumstances. CLASH was built to help rectify this discrepancy.

Focus of this study

This is by no means a comparable exercise to the research being done with CLASH —– but is more of a study in experimentation and correlation building within R frameworks. For this study I am using NYC weather data, and crime occurrences within a 9 month time period from 1-01-2015 to 09-30-2015. Below is an overview, and visualization of both.

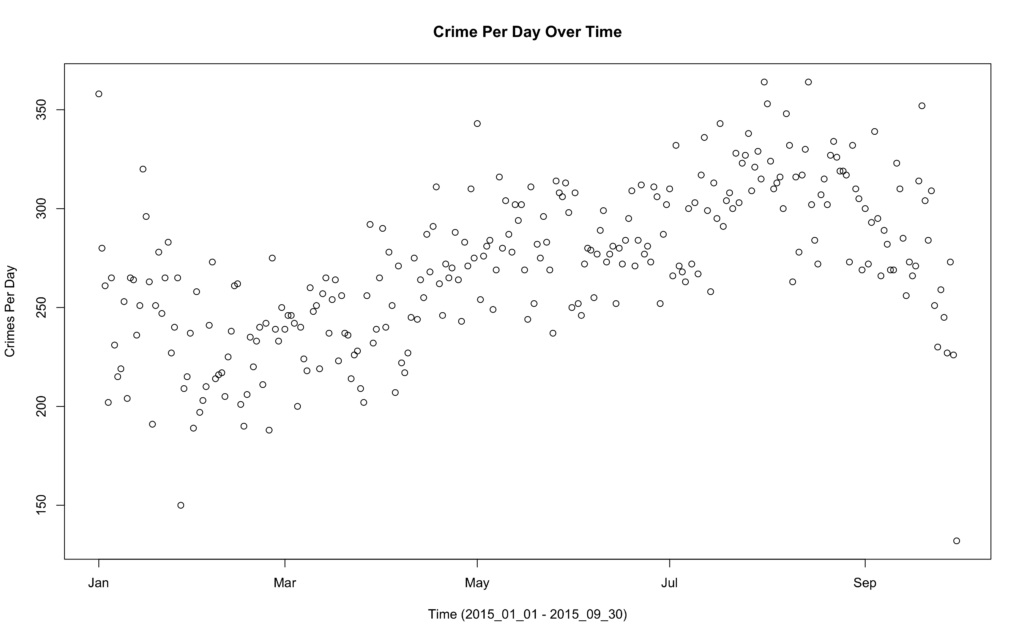
Crime

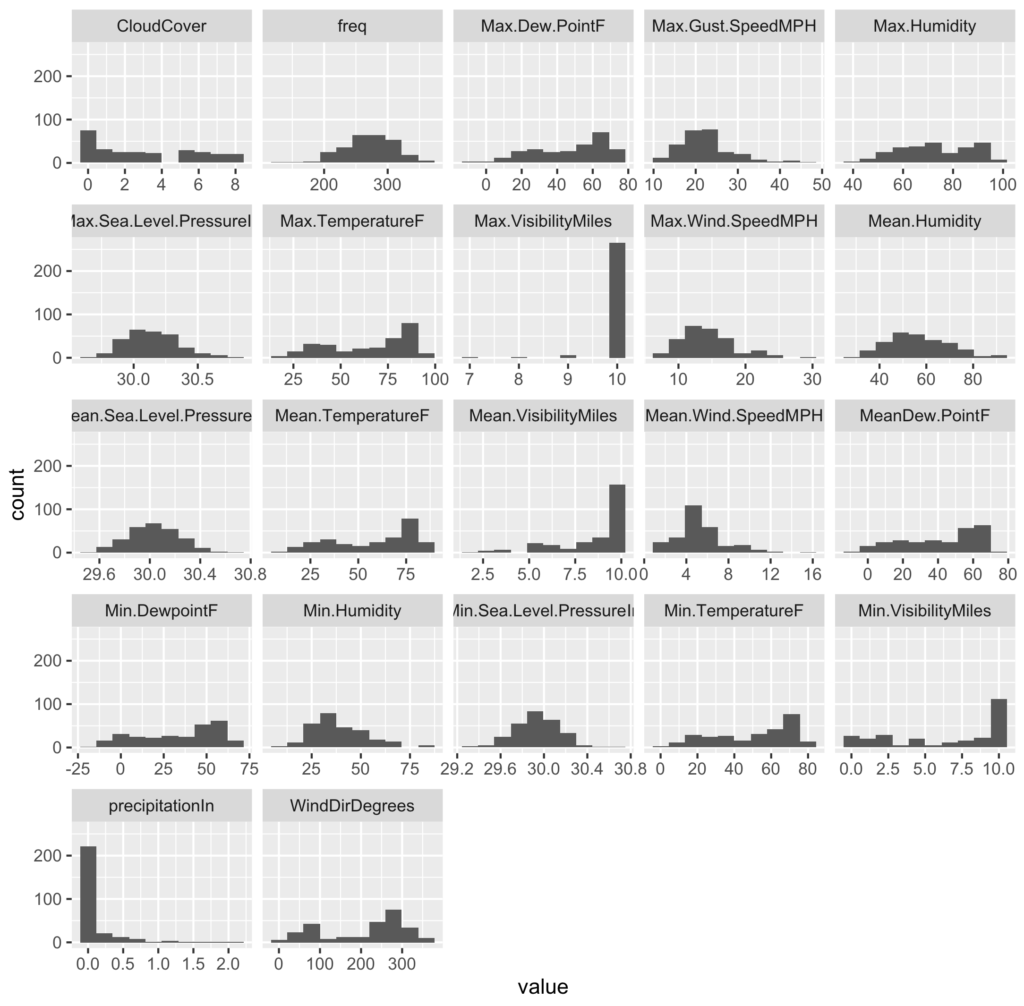
Weather

Model Experimentation

The areas I need to investigate are the correlation of crime frequency (noted as “freq” in my variables) to the weather data variables. This includes a small cleaning effort of counting crime per dates, merging tables, and transforming data-types (numeric, integer, character).

# Global Variables

library(plyr)
library(corrplot)
library(tidyverse)
library(caret)
library(scatterplot3d)
library(psych)
library(tidyr)

weather = read.csv("/Users/SETHCRIDER/Desktop/NYC_weather.csv")
nypd = read.csv("/Users/SETHCRIDER/Desktop/NYPD_7_Major_Felony_Incidents.csv")

dats=seq(as.Date("2015-01-01"),as.Date("2015-12-31"),by=1)
fdats=as.Date(nypd$Occurrence.Date, format="%m/%d/%Y")
tab <- cbind(nypd, date = fdats)

summary(weather)
datsweather=as.Date(weather$EST, format="%m/%d/%Y") 
weatherappend <- cbind(weather, date = datsweather)
weatherappend <- weatherappend[-c(274:365),]

__________________________________________________________________________

# Model of Daily Aggregate Crime Frequency to Weather Factors 

tabfilter = tab[which(tab$date>='2015-01-01'),c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21)]
tabfilter = tabfilter[-c(274:365),]
a = table(tabfilter$date)
b = as.data.frame(a)
colnames(b) <- c("date","freq")
b <- b[c("freq","date")]

DayCount = table(tabfilter$date)
CrimeCount =  table(tabfilter$Offense)

df<-cbind(weatherappend, freq = b$freq)
v = as.factor(df$PrecipitationIn)
v = gsub("T", 0.1, v)
v= as.numeric(v)

df<-cbind(df, precipitationIn = v)

nums <- unlist(lapply(df, is.numeric))  
mcor <- df[ , nums]
mydata.cor = cor(mcor)
quartz()
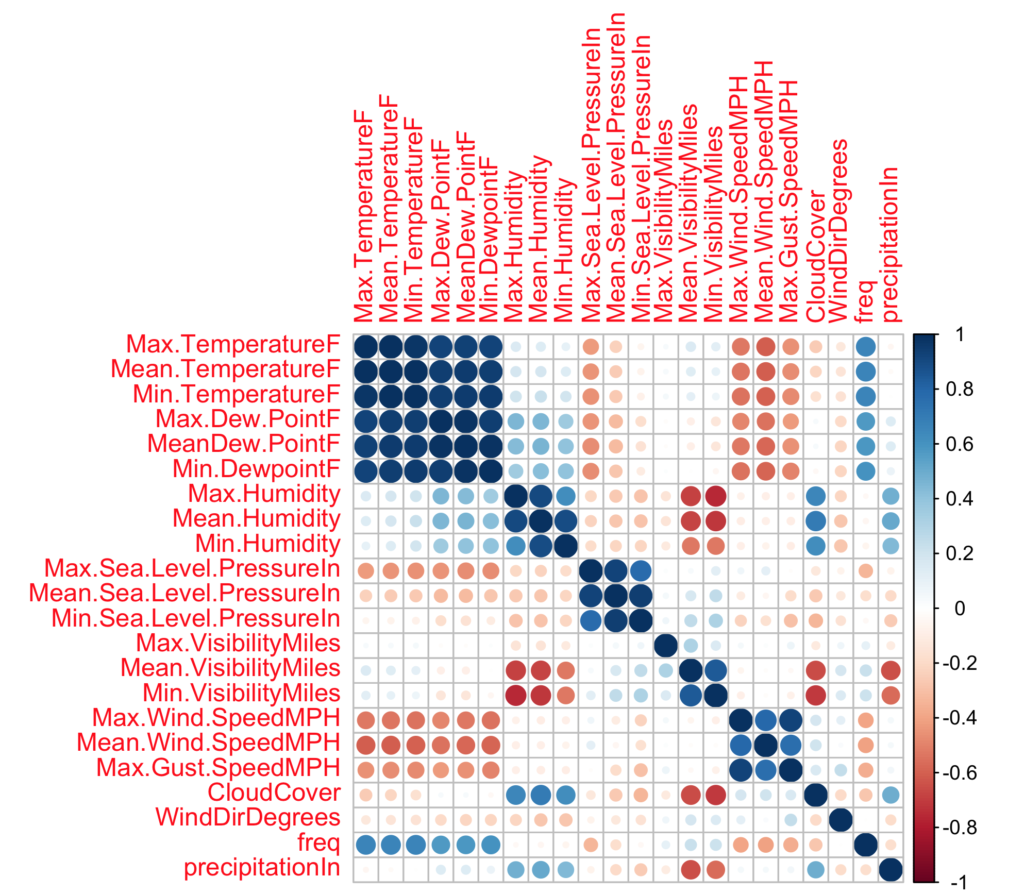
corrplot(mydata.cor)

From this point, I plotted a correlation matrix to see which variables could be likely candidates for building a linear, and multiple regression model. Keep in mind that the scale is 1 for positively correlated and -1 for negatively correlated. From these initial results, it seems my daily crime frequency is more closely related to temperature than to other variables.

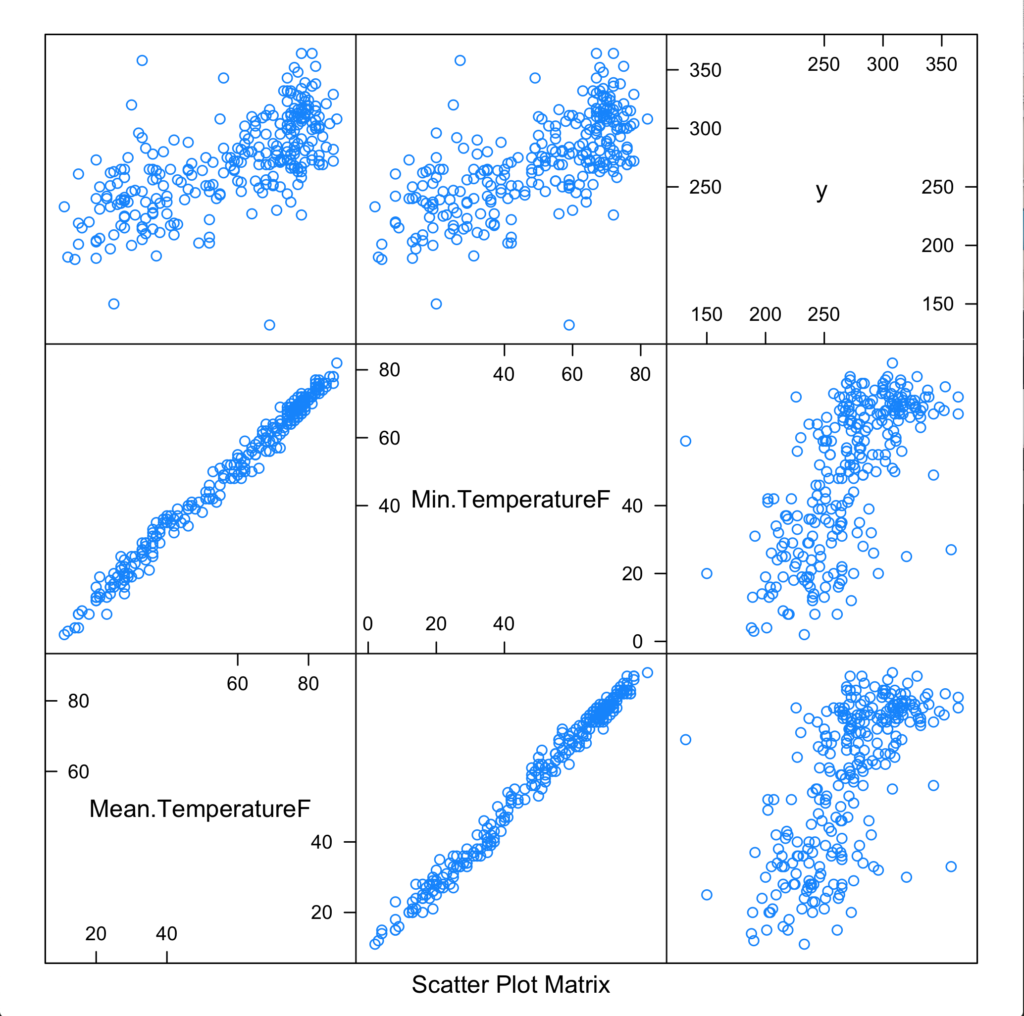
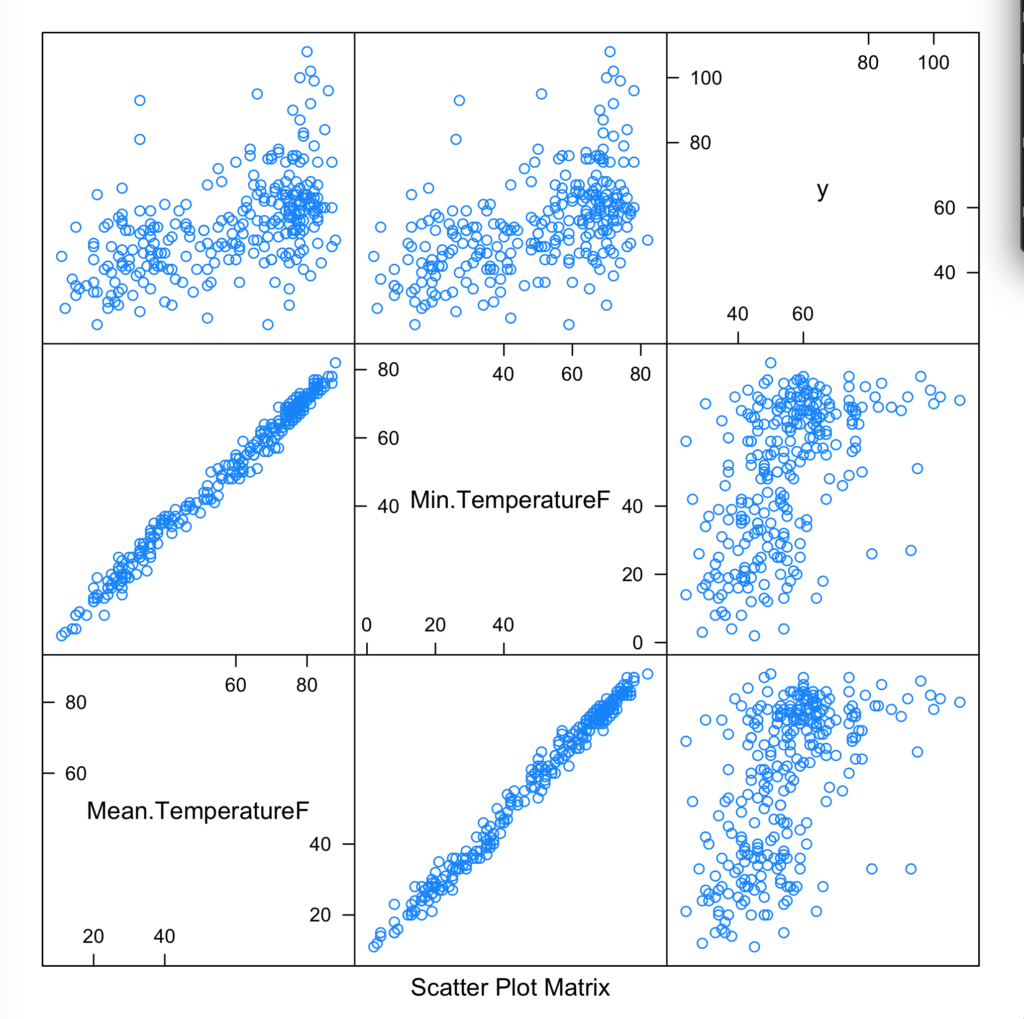
Just how close? Let’s take a look with a scatter plot matrix —- remember y is our daily crime frequency.

It seems from this initial scoring that our correlation is loose at best, so our models should be approached with apprehension. Considering our experiment here is mostly an informative exercise—- we soldier onward!

Building model 1 and model 2

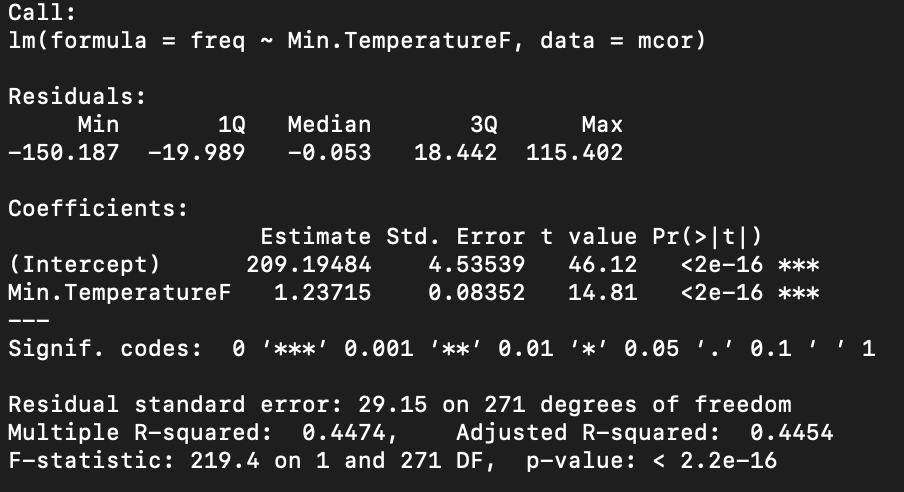
model<-lm( freq ~ Min.TemperatureF, mcor)
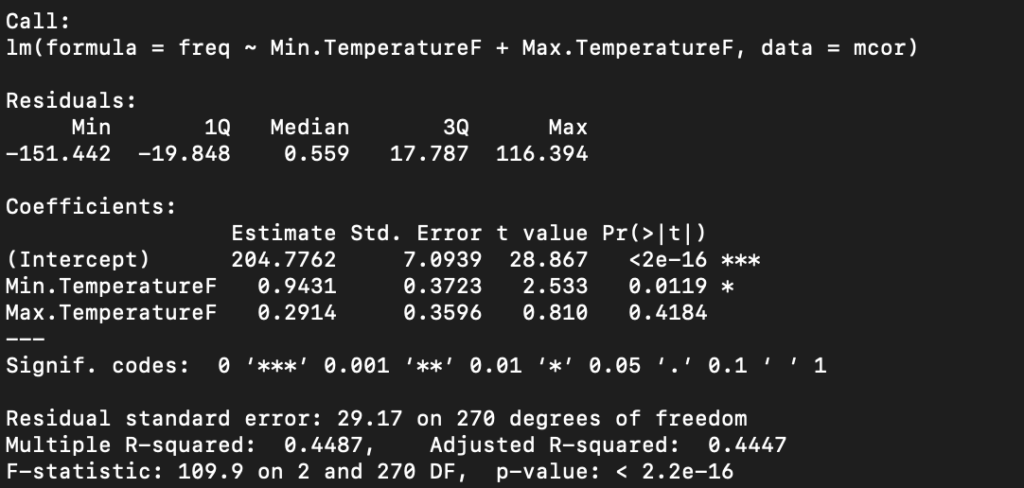
model1<- lm( freq ~ Min.TemperatureF+Max.TemperatureF, mcor)

I decided to build two models from the temperature to compare and contrast with each other, and see the state of our performance and predictions. One is purely linear, and the other is a multiple regression approach.

Model: Frequency by Min.Temperature

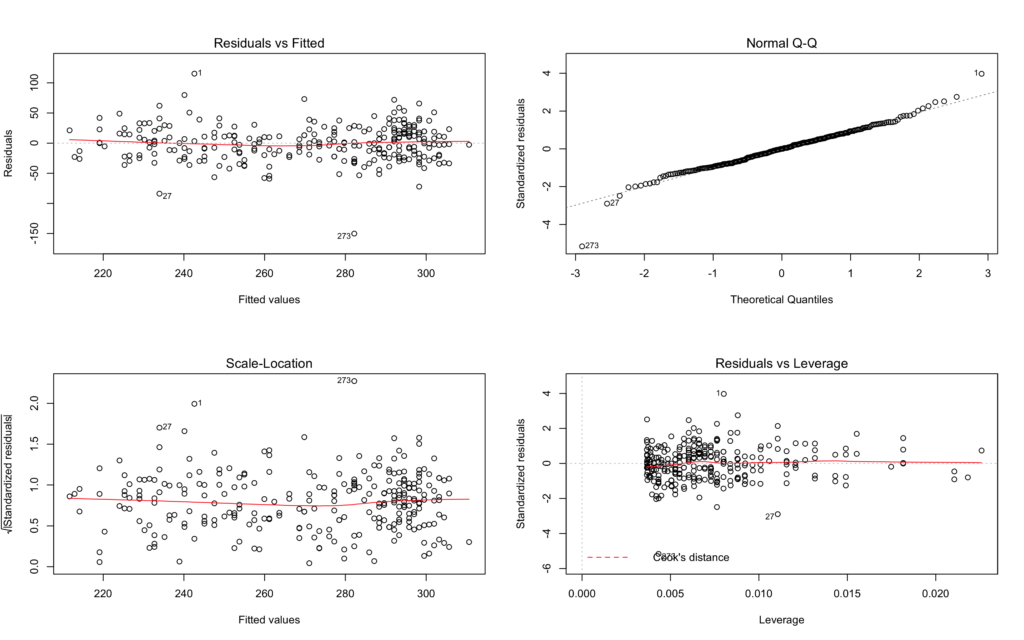
Model2: Frequency by Min.TemperatureF, and Max.TemperatureF

Anova test

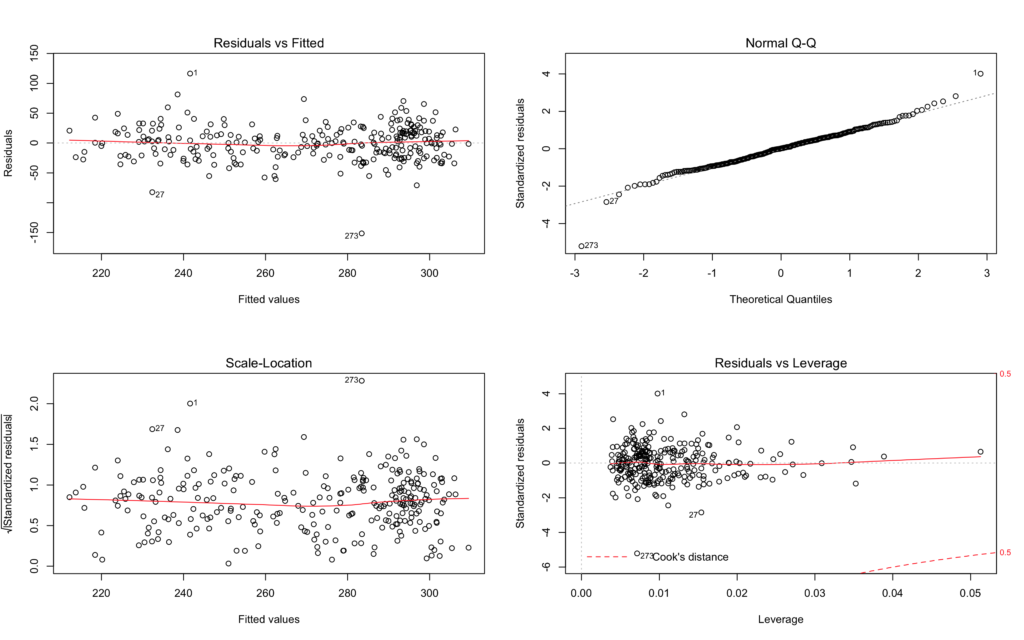
The results of the anova test show no significant statistical differences between them. If we consult the residual tables for both in the images above you can see how closely related they appear.

For the sake of ease— I decided to narrow in on the first model with one variable to continue the experiment.

Graphing Our Model

quartz()
pred.int <- predict(model, interval = "prediction")
mydata <- cbind(mcor, pred.int)
p <- ggplot(mydata, aes(Min.TemperatureF, freq)) +
  geom_point() +
  stat_smooth(method = lm)
  p + geom_line(aes(y = lwr), color = "red", linetype = "dashed")+
    geom_line(aes(y = upr), color = "red", linetype = "dashed")

min(mcor$Min.TemperatureF)
max(mcor$Min.TemperatureF)

Min.TemperatureF <- seq(2,82, by=1) 
freq <- seq(132,364, by=1) 
pred_grid <- expand.grid(Min.TemperatureF = Min.TemperatureF, freq = freq)

quartz()
pred_grid$freq2 <-predict(model, new = pred_grid)
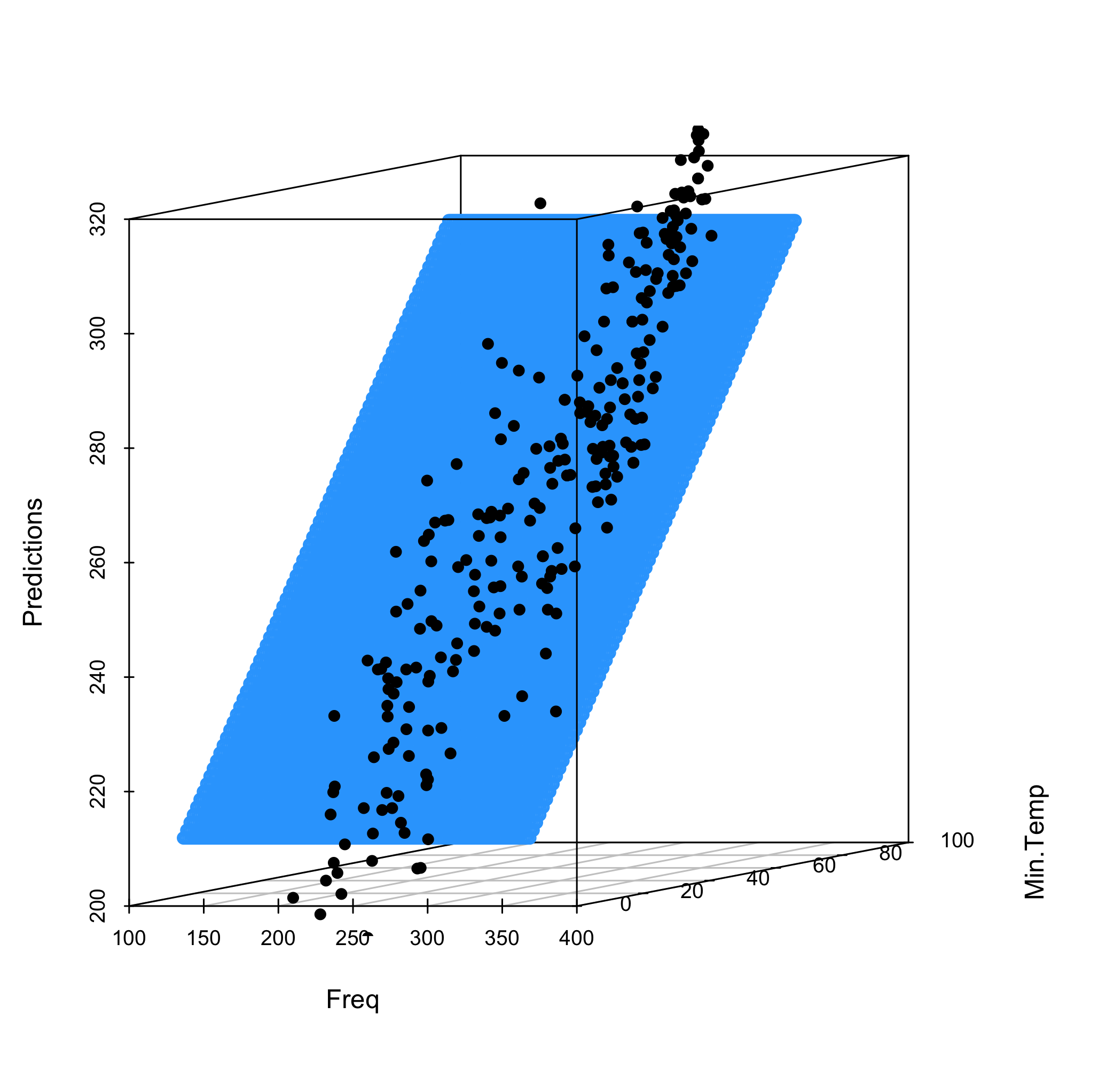
fit_2_sp <- scatterplot3d(pred_grid$freq, pred_grid$Min.TemperatureF, pred_grid$freq2, angle = 10, color = "dodgerblue", pch = 1, ylab = "Min.Temp", xlab = "Freq", zlab = "Predictions" )
fit_2_sp$points3d(mcor$freq, mcor$Min.TemperatureF, mcor$freq, pch=16)

quartz()
ggplot(mcor, aes(Min.TemperatureF, freq, col=freq)) + geom_point() +
             geom_smooth(method="lm", se=FALSE) + facet_wrap(~freq)

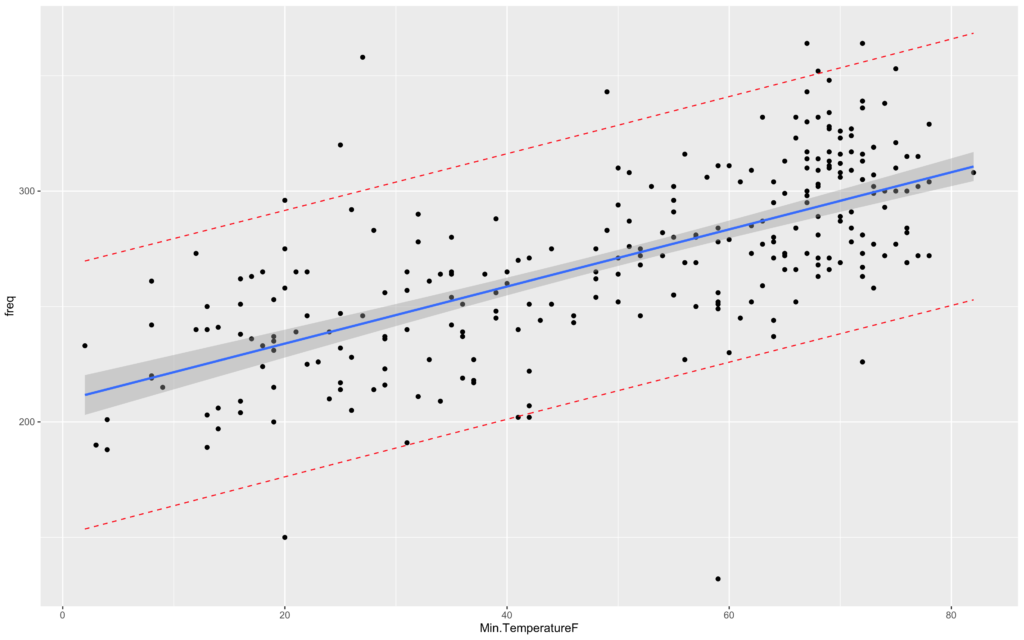
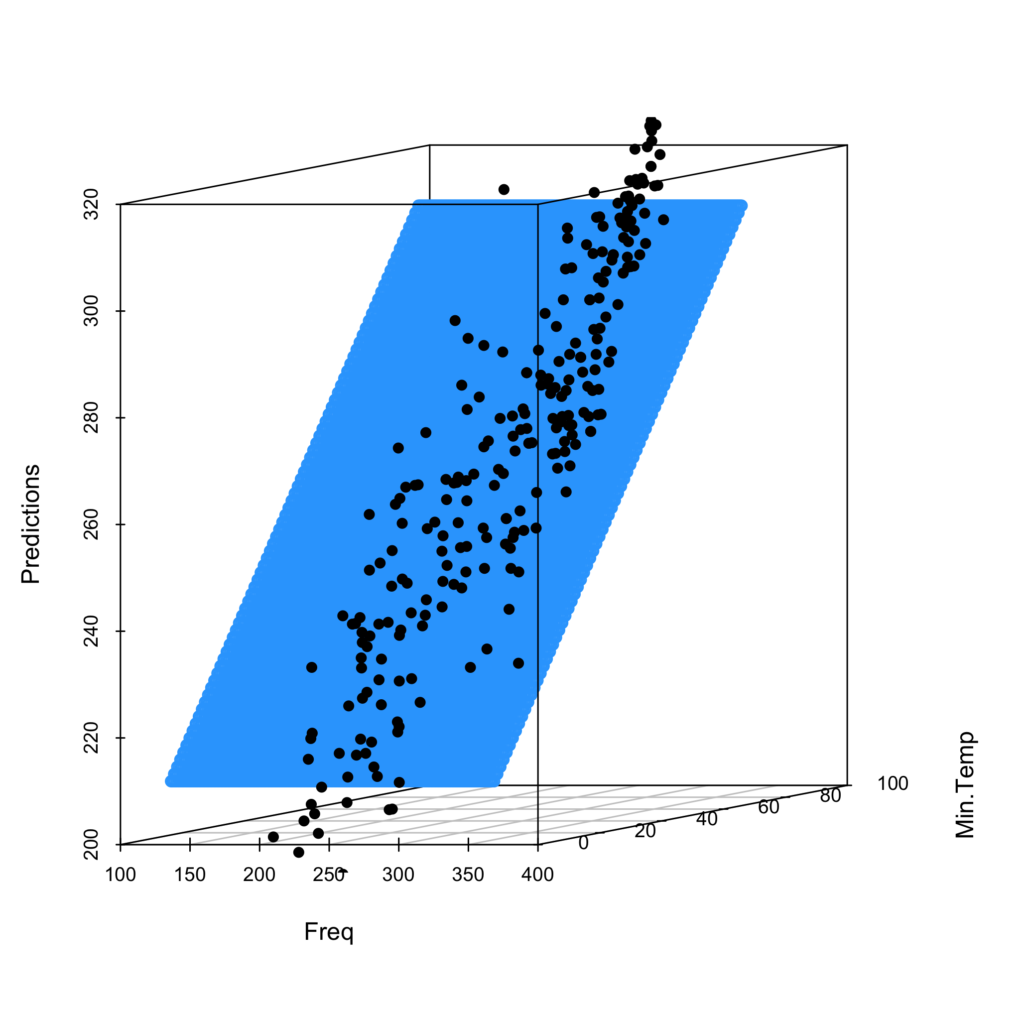
Predicting with the Model

So our model is far from great. But we can still throw predictions for the fun of it and see what the results are.

newdatamodel = data.frame( 
Min.TemperatureF=70)

newdatamodel1= data.frame( 
Max.TemperatureF=80, 
Min.TemperatureF=70)

predict(model,newdatamodel)
predict(model1,newdatamodel1)

For the first model, the predicted frequency for a Min.temperature of 70 is:

295.7956 crimes per day

The second model, the predicted frequency for a Min.Temperature of 70, and a Max.Temperature of 80 is:

294.108 crimes per day

Not a huge difference! Both do seem to be functioning within the same realm. Interesting…

What About Specific Crimes?

This is a good consideration. Let us run the process again but with daily frequencies adjusted for each crime classification, and reference our correlation table.

# Global Variables

library(plyr)
library(corrplot)
library(tidyverse)
library(caret)
library(scatterplot3d)
library(psych)
library(tidyr)

weather = read.csv("/Users/SETHCRIDER/Desktop/NYC_weather.csv")
nypd = read.csv("/Users/SETHCRIDER/Desktop/NYPD_7_Major_Felony_Incidents.csv")

dats=seq(as.Date("2015-01-01"),as.Date("2015-12-31"),by=1)
fdats=as.Date(nypd$Occurrence.Date, format="%m/%d/%Y")
tab <- cbind(nypd, date = fdats)

summary(weather)
datsweather=as.Date(weather$EST, format="%m/%d/%Y") 
weatherappend <- cbind(weather, date = datsweather)
weatherappend <- weatherappend[-c(274:365),]

_____________________________________________________________________

# Model of Offense Types (Frequency) and correlation to weather factors 

UN=unique(nypd$Offense)
dcounts=matrix(ncol=length(UN),nrow=length(dats))
for (i in 1:length(dats))
{
for (j in 1:length(UN))
{
dcounts[i,j]=length(which(fdats==dats[i] & nypd$Offense==UN[j]))
}
}

dcounts=data.frame(dcounts)
dcounts <- cbind(dcounts, date = dats)
dcounts <- dcounts[-c(274:365),]
names(dcounts)<-c("MURDER","RAPE","ROBBERY","FEL_ASSAULT","BURGLARY","GRAND_LR","GRAND_LR_MV","date")

dcounts<-cbind(dcounts, df)
nums <- unlist(lapply(dcounts, is.numeric)) 
mcor <- dcounts[ , nums]
mydata.cor = cor(mcor)
corrplot(mydata.cor)

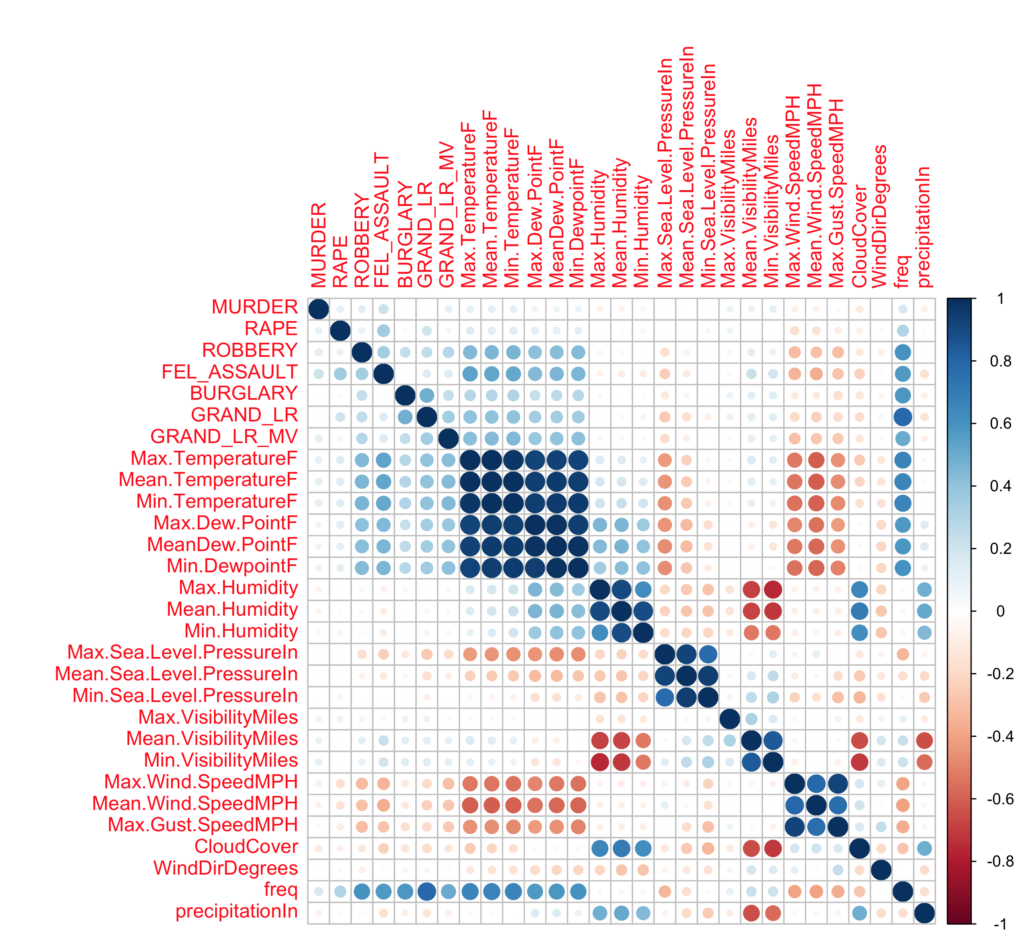
Robbery, and Felony Assault seem to have the strongest correlation to —–no surprise here—- temperature. However it is very poor. For this experiment, I am going to focus solely on Felony Assault and try to model it anyway.

Felony Assault Model and Evaluation

model3: Felony Assault Frequency by Min.Temperature and Max.Temperature

model3< lm(mcor$FEL_ASSAULT~mcor$Min.TemperatureF+mcor$Max.TemperatureF)
 

quartz()
par(mfrow=c(2,2)) 
plot(model2) 
summary(bi)

ggplot(mcor) + 
  geom_jitter(aes(FEL_ASSAULT,Min.TemperatureF), colour="blue") + geom_smooth(aes(FEL_ASSAULT,Min.TemperatureF), method=lm, se=FALSE) +
  geom_jitter(aes(FEL_ASSAULT,Max.TemperatureF), colour="green") + geom_smooth(aes(FEL_ASSAULT,Max.TemperatureF), method=lm, se=FALSE) +
  labs(x = "", y = "")

quartz()
ggplot(mcor, aes(Min.TemperatureF, FEL_ASSAULT, col=freq)) + geom_point() +
             geom_smooth(method="lm", se=FALSE) + facet_wrap(~FEL_ASSAULT)

quartz()
ggplot(mcor, aes(Max.TemperatureF, FEL_ASSAULT, col=freq)) + geom_point() +
             geom_smooth(method="lm", se=FALSE) + facet_wrap(~FEL_ASSAULT)

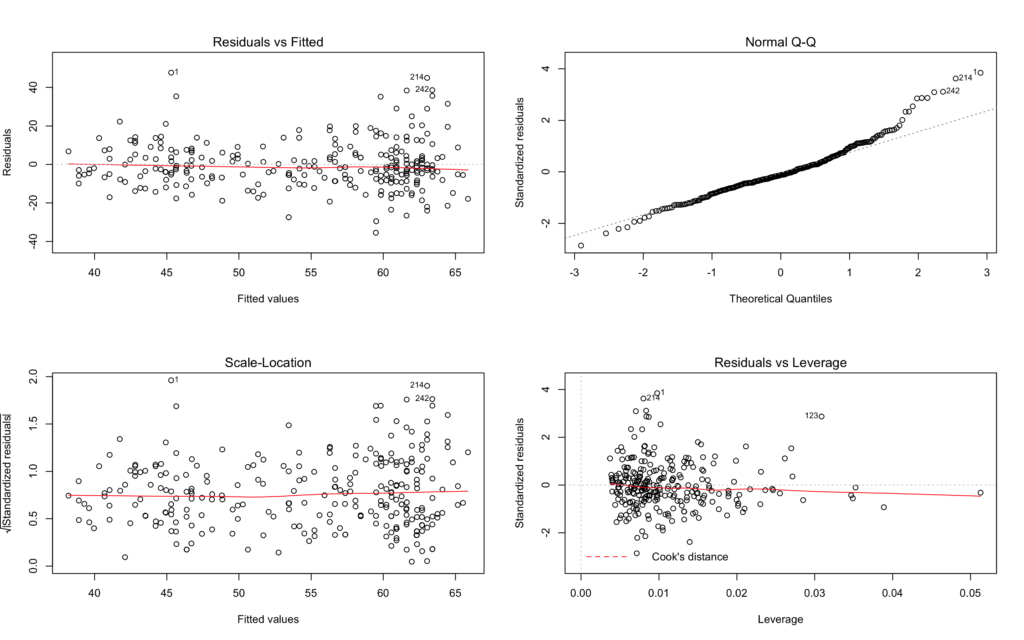
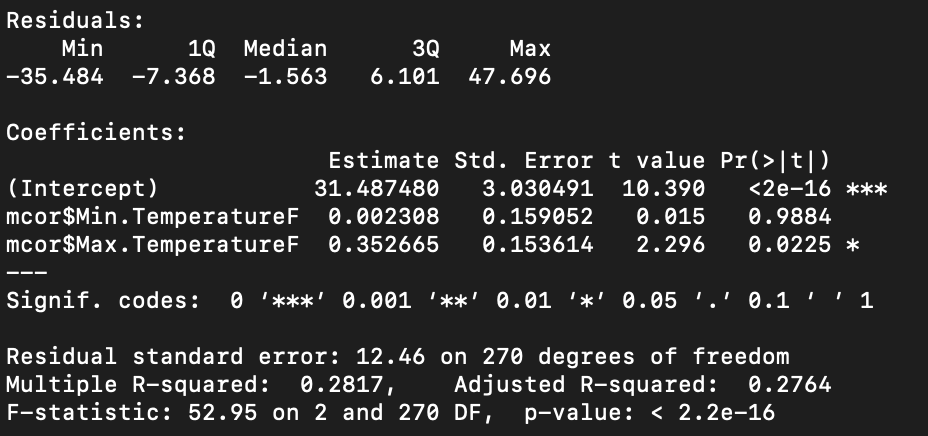
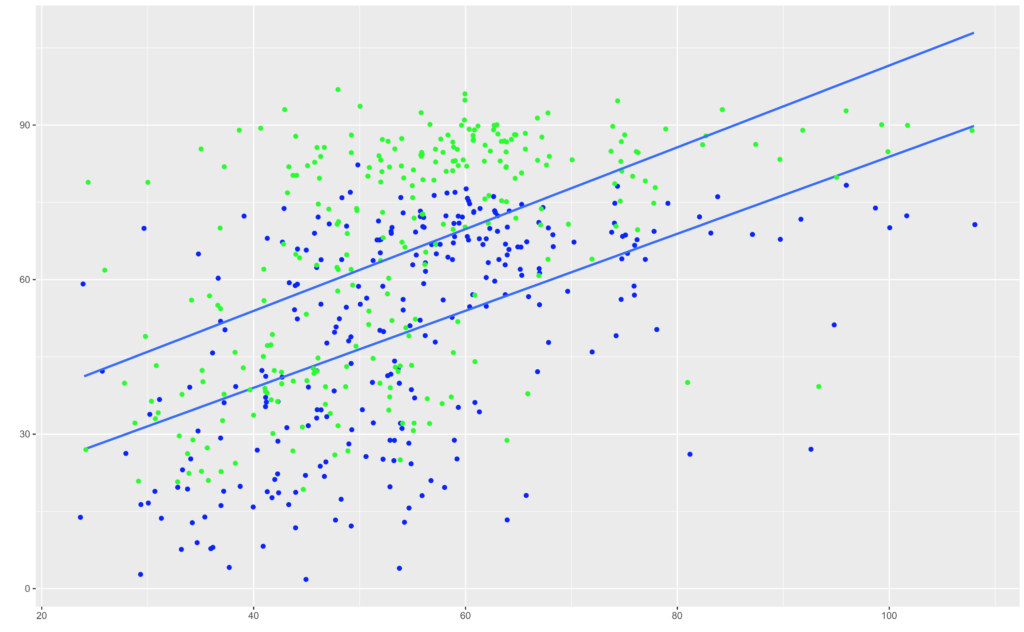
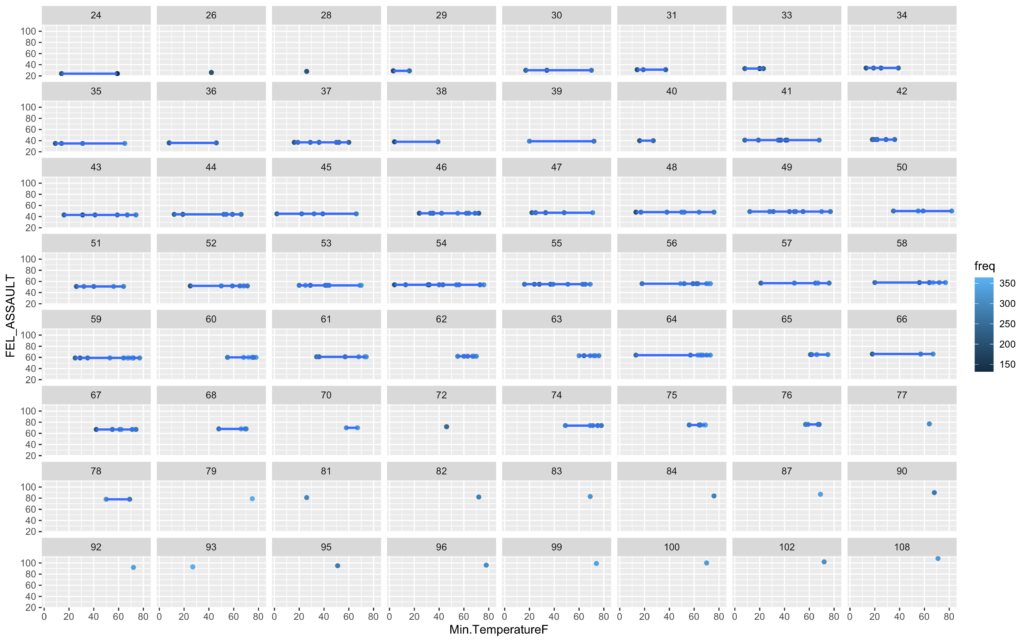
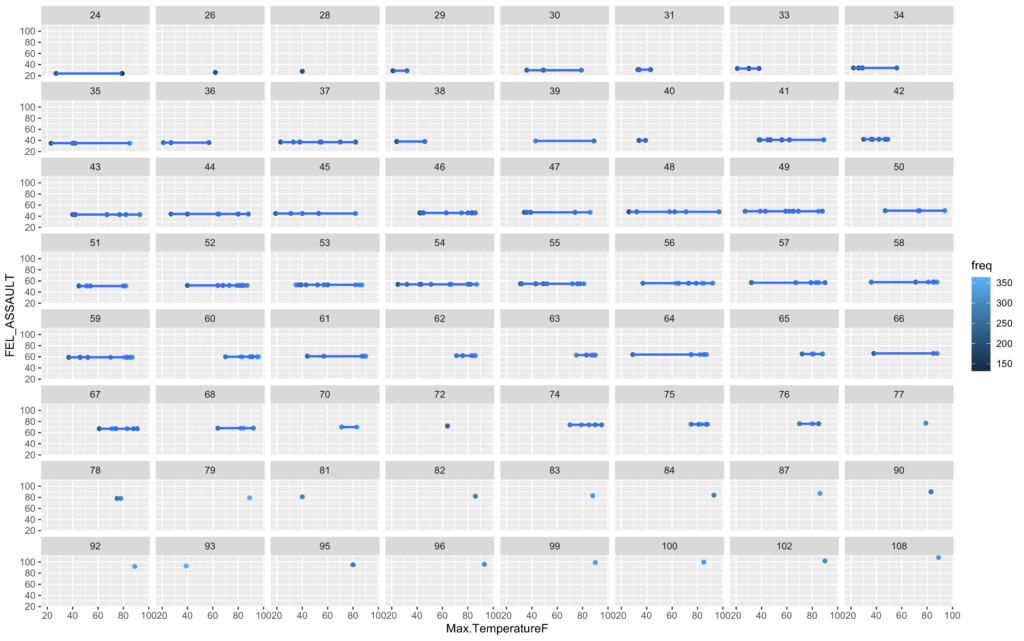
This is a poor model and it seems we just do not have enough information in these two data sets to justify any sort of answer from the algorithm. The variance is just too high.

Conclusions

Long story short:

Using simple variable and crime frequencies hasn’t produced anything ground breaking. Is there enough teeth, and correlation to focus on?—I think there is—– but it will take more more meaningful social, and environmental variables, as well as a longer recorded time span.

Keep in mind that there is not one correct approach to build a model. The considerations should depend on use case and what is being effected by predictions/performance. Only you can derive the standard for which you measure, and rate evaluation. For an experiment like this, there is no harm forging ahead to build a poor model if only to learn, and improve upon the next!